About Calculation of Edge Load Inertia

This is a calculation example for having inertia (moment of inertia) of edge load.

If you use your CAD for designing a gripper, use it for calculating the value.

Edge load is a combination of an end effector like a gripper for robot flange and a work.

Calculation of edge load inertia will be used at the cases as follows.

• You should not put edge load beyond the "maximum allowable inertia" in the specification of the robot.
• Inputting a condition of edge load into use condition parameter within a project will make "Gravity Compensation Control Function (GrvCtrl)" and "Optimum Speed Control Function (SpeedMode)" motions more smooth. * Attention

Calculation Formula of Inertia (Moment of Inertia)

There are basic calculation formulas of inertia for each figure (cylinder1, cylinder2, cuboid, sphere, position of gravity center is not on rotation axis.

• l : Inertia (rotation moment)
• m : Mass
• r : Radius
• a, b, c, L : Length

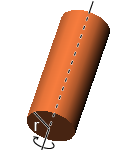
Cylinder1 (Rotate Around Central Axis of Circle)

Central axis of the circle is the rotation center.

Formula l = 1/2 * m * r^2

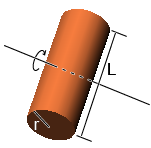
Cylinder2 (Rotate Around the Axis which is Perpendicular to the Central Axis of Circle)

Rotation axis is across the gravity center.

Formula l = 1/4 * m * ( r^2 + 1/3 * L^2)

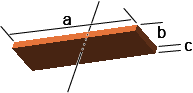
Cuboid

Rotation axis is across the gravity center.

Formula l = 1/12 * m * ( a^2 + b^2 )

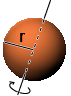
Sphere

Rotation axis is across the gravity center.

Formula l = 2/5 * m * r^2

When the Position of Gravity Center is not on the Rotation Axis

lg：Inertia around gravity center

Formula l = lg + m * L^2

Example of Calculation of Inertia Around J4/J5/J6

We use the following end effector for the example.

PartA

Radius (ra):20, Length (la):100, Mass (ma):1.0, Length from the rotation axis to gravity center (La)

PartB

Radius (rb):10, Length (lb):40, Mass (mb):0.1, Length from the rotation axis to gravity center (Lb)

PartC

Length (hc):120, Width (wc):15, Thickness (tc):10, Mass (mc):0.14, Length from the rotation axis to gravity center (Lc)

Inertia Around J6 (Ij6)

Inertia around J6 at PartA is

Ia6 = 1/2 * ma * ra^2 + ma * La^2

Inertia around J6 at PartB is

Ib6 = 1/2 * mb * rb^2 + mb * Lb^2

Inertia around J6 at PartC is

Ic6 = 1/12 * mc * (hc^2 + wc^2) + mc * Lc^2

Inertia around J6 at entire gripper is

Ij6 = Ia6 + Ib6 + Ic6

Inertia Around J5 (Ij5)

As to the length from the rotation axis of each part to gravity center, refer to the drawing of the robot for calculation. As to the inertia around J5 and J4, the length from gravity center depends on the axis position below the relevant axis. Calculation should be done using the position with maximum length.

Inertia around J5 at PartA should be the rotation axis which is perpendicular to the central axis of the cylinder.

Ia5 = 1/4 * ma * (ra^2 + 1/3 * la^2) + ma * La^2

Inertia around J5 at PartB should be the rotation axis which is perpendicular to the central axix of the cylinder.

Ib5 = 1/4 * mb * (rb^2  + 1/3 * lb^2) + mb * Lb^2

Inertia around J5 at PartC is

Ic5 = 1/12 * mc * (wc^2 + tc^2) + mc * Lc^2

Inertia around J5 at entire gripper is

Ij5 = Ia5 + Ib5 + Ic5

Inertia Around J4 (Ij4)

J4 will be calculated similar to J5's case.